OpenMP Directives
Assignment
Report
Matrix Multiplication (mm)
Directives
I used a parallel do for the outer loop of the matrix initialization. There is no dependency since data is only written. I did not make the inner loop parallel because each thread should have some work to do, not only setting 2 array elements.
I also used a parallel do for the outer loop of the matrix multiplication. There is no data dependency, since data is only read from arrays a and b and only written to array c. Again, I only used the outer loop to put enough work into one thread and avoid excessive overhead through thread creation.
Speed-up Data

Speed-up Data Plots
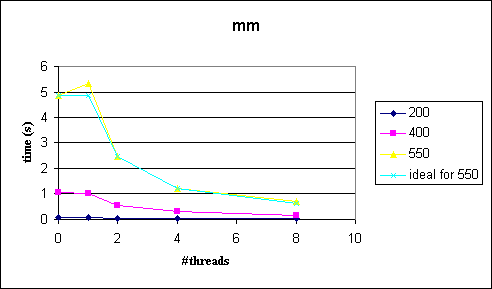
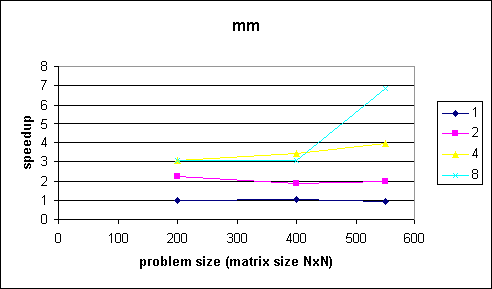
Comments
Since calculation is very independent, each chunk of work is equally hard and the OpenMP overhead is quite small we are able to achieve a almost optimal speedup (see "550"-"ideal for 550" in first figure). So, I guess the point is that we can really simply get very good speedup results with OpenMP.
Source Code
mm.f: See end of report
Mandelbrot Calculation (mandel)
Directives
I used a parallel for construct for the outermost loop of the calculation, which is decomposition at row level. The reason was as before: Enough work for each thread. I think making the inner loop parallel would introduce too much overhead (thread creation).
Speed-up Data

Speed-up Data Plots
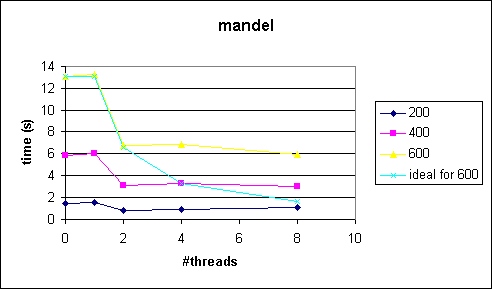

Comments
As can be seen from the figures the speedup is really bad. This is because the workload of each pixel is different and we are using a static decomposition. See section 5 (Extra Credit A) for a better solution.
Source Code
mandel.c: See end of report
2D Heat Equation (heat2d)
Directives
Again, I used a parallel for to parallize only one loop, for the same reasons as stated in the previous examples. But this time it was not the outermost loop, because it can't be parallized, as explained in addendum of Homework 3. Therefore I took the second but outermost loop.
Speed-up Data
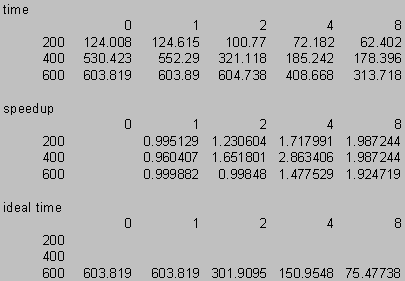
Speed-up Data Plots
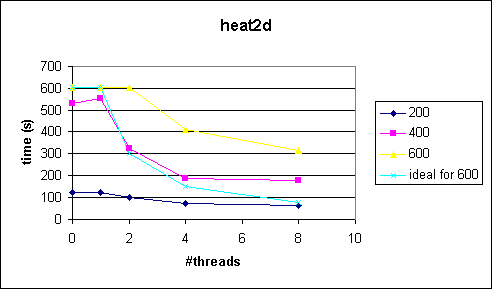
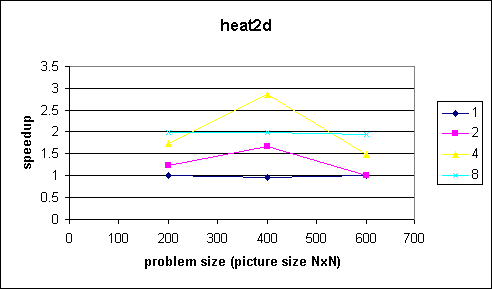
Comments
The problem in this example is that the outermost loop can not be parallized. We therefore pay the thread management overhead in every iteration of the outermost loop. Since the program takes quite a while to execute we can see what happens at small problem sizes.
Source Code
heat2d: See end of report
Poor Parallelization
Below are some test results to show how bad it is to have a large serial outer loop (iterations, fixed) and a small, but parallized, inner loop (problem size). As you can see, the speedup stays below 1 and even drops with the number of threads. Therefore don't parallize this kind of problem.

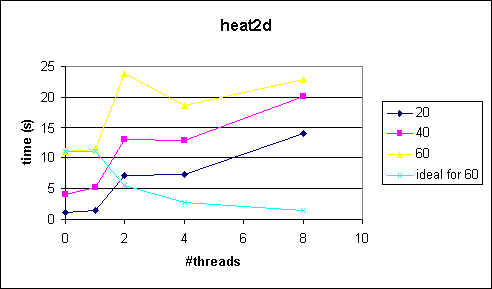
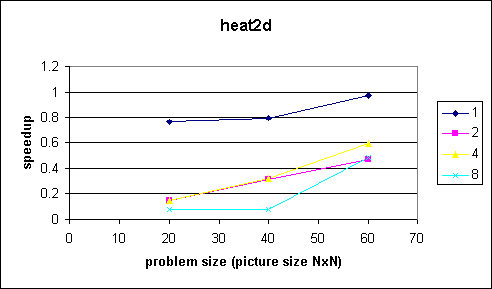
Comments and Conclusions
Parallezing code with OpenMP is really simple. One can concentrate on what to make parallel and leave the how to the compiler. PVM seems like an "assembler language," while OpenMP lifts parallelism to compiler level. But, as usual, you pay some overhead penalty for the convenience and portability.
When moving from a cluster to a shared memory architecture one must be aware that smaller decomposition sizes are possible and useful since the communication overhead is much smaller.
The ideal times given are calculated by serial_time/number_of_threads.
Extra Credit A (dynamic mandel)
Directives
I used the same directives as for the former test (see section 2, Mandelbrot Calculation (mandel)). In addition I specified a dynamic schedule with a chunk size of 5.
Speed-up Data

Speed-up Data Plots
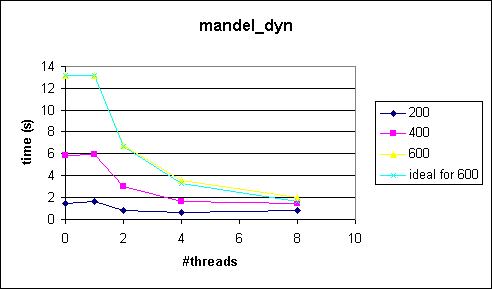

Comments
As expected, the dynamic schedule balanced the workload for the threads. The main problem was to find a reasonable chunk size. I used a simple trial-and-error approach to find a good chunk size. The minimum problem size is 200 and we have at most 8 threads. So, starting with a chunk size of 25 (=200/8) seemed reasonable. I changed the chunk size from 25 to 20, 10 and finally 5, which gave a good result, ie almost optimal speedup (see first figures). So, the point is to balance the workload through dynamic decomposition.
Source Code
mandel_dyn.c: See end of report
Source Code
mm.f
* A program to multiply two matrices
*
* the program requests the user enter the dimensions of the matrices.
* it then allocates space for the arrays and initializes them.
* a timing function computes the elapsed time for the matrix multiply
*
program main
************************************************************
implicit none
integer n,m
double precision , dimension (:, :), ALLOCATABLE :: a,b,c
double precision sum
integer i,j,k
integer status
real gettime
integer, dimension(8):: tdat
double precision :: t1, t2, et
*
* Read dimension information
*
write(*,*) "Input array dimension n"
read(5,*) n
*
* allocate arrays dynamically
*
allocate (a(n, n), STAT = status)
if (status > 0) then
print*, "allocation error"
stop
endif
allocate (b(n, n), STAT = status)
if (status > 0) then
print*, "allocation error"
stop
endif
allocate (c(n, n), STAT = status)
if (status > 0) then
print*, "allocation error"
stop
endif
call initialize (n,a,b)
t1=gettime();
*
* multiply the matrices
*
!$omp parallel do private(i,j,sum,K) shared(a,b,c)
do i=1,n
do j = 1,n
sum = 0
do K=1,n
sum = sum + a(i,k)*b(k,j)
enddo
c(i,j) = sum
enddo
enddo
t2=gettime();
et = t2-t1
print*, "Dimension: ", n, " time: ",et
* do i=1,n
* do j=1,n
* print*, c(i,j)
* enddo
* enddo
stop
end
subroutine initialize (n,u,v)
******************************************************
* Initializes data
*
******************************************************
implicit none
integer n
double precision u(n,n),v(n,n)
integer omp_get_thread_num
integer i,j
* Initilize initial condition and RHS
!$omp parallel do private(j,i) shared(u,v)
do j = 1,n
do i = 1,n
u(i,j) = i+j
v(i,j) = i-j
enddo
enddo
return
end
real function gettime()
integer, dimension(8):: tdat
CALL DATE_AND_TIME(VALUES=tdat)
gettime=tdat(5)*3600 + tdat(6)*60+ tdat(7)+tdat(8)/1000.0
return
end
mandel.c
#include <stdio.h>
#include <string.h>
#include <math.h>
#define X_RESN 800 /* x resolution */
#define Y_RESN 800 /* y resolution */
#define X_MIN -2.0
#define X_MAX 2.0
#define Y_MIN -2.0
#define Y_MAX 2.0
typedef struct complextype
{
float real, imag;
} Compl;
int main ( int argc, char* argv[])
{
/* Mandlebrot variables */
int i, j, k;
Compl z, c;
float lengthsq, temp;
int maxIterations;
int res[X_RESN][Y_RESN];
/* Calculate and draw points */
maxIterations = atoi( argv[1] );
#pragma omp parallel for shared(res,maxIterations) private(i,j,z,c,k,temp,lengthsq)
for(i=0; i < Y_RESN; i++)
for(j=0; j < X_RESN; j++) {
z.real = z.imag = 0.0;
c.real = X_MIN + j * (X_MAX - X_MIN)/X_RESN;
c.imag = Y_MAX - i * (Y_MAX - Y_MIN)/Y_RESN;
k = 0;
do { /* iterate for pixel color */
temp = z.real*z.real - z.imag*z.imag + c.real;
z.imag = 2.0*z.real*z.imag + c.imag;
z.real = temp;
lengthsq = z.real*z.real+z.imag*z.imag;
k++;
} while (lengthsq < 4.0 && k < maxIterations);
if (k >= maxIterations) res[i][j] = 0;
else res[i][j] = 1;
}
printf("%d\n", res[0][0]);
/* Program Finished */
return 0;
}
heat2d.c
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define CRESN 302 /* x, y resolution */
#define RESN 300
#define MAX_COLORS 8
#define MAX_HEAT 20.0
double solution[2][CRESN][CRESN], diff_constant;
int cur_gen, next_gen;
double sim_time, final = 10000.0, time_step = 0.1, diff = 10000.0;
void compute_one_iteration (double);
void setup ();
void
main (int argc, char *argv[])
{
int temp;
/* set window position */
/* Calculate and draw points */
setup ();
for (sim_time = 0; sim_time < final; sim_time += time_step)
{
compute_one_iteration (sim_time);
temp = cur_gen;
cur_gen = next_gen;
next_gen = temp;
}
}
void
setup ()
{
int i, j;
#pragma omp parallel for shared(solution) private(i,j)
for (i = 0; i < CRESN; i++)
for (j = 0; j < CRESN; j++)
solution[0][i][j] = solution[1][i][j] = 0.0;
cur_gen = 0;
next_gen = 1;
diff_constant = diff * time_step / ((float) RESN * (float) RESN);
}
void
compute_one_iteration (double t)
{
int i, j;
/* set boundary values */
for (i = 0; i < CRESN; i++)
{
if (i < 256 || i > 768)
solution[cur_gen][i][0] = solution[cur_gen][i][1];
else
solution[cur_gen][i][0] = MAX_HEAT;
}
for (i = 0; i < CRESN; i++)
{
solution[cur_gen][i][CRESN - 1] = solution[cur_gen][i][CRESN - 2];
}
for (i = 0; i < CRESN; i++)
{
solution[cur_gen][0][i] = solution[cur_gen][1][i];
solution[cur_gen][CRESN - 1][i] = solution[cur_gen][CRESN - 2][i];
}
/* corners ? */
#pragma omp parallel for shared(solution,cur_gen,next_gen,diff_constant) private(i,j)
for (i = 1; i <= RESN; i++)
for (j = 1; j <= RESN; j++)
solution[next_gen][i][j] = solution[cur_gen][i][j] +
(solution[cur_gen][i + 1][j] +
solution[cur_gen][i - 1][j] +
solution[cur_gen][i][j + 1] +
solution[cur_gen][i][j - 1] -
4.0 * solution[cur_gen][i][j]) *
diff_constant;
}
mandel_dyn.c
#include <stdio.h>
#include <string.h>
#include <math.h>
#define X_RESN 800 /* x resolution */
#define Y_RESN 800 /* y resolution */
#define X_MIN -2.0
#define X_MAX 2.0
#define Y_MIN -2.0
#define Y_MAX 2.0
typedef struct complextype
{
float real, imag;
} Compl;
int main ( int argc, char* argv[])
{
/* Mandlebrot variables */
int i, j, k;
Compl z, c;
float lengthsq, temp;
int maxIterations;
int res[X_RESN][Y_RESN];
/* Calculate and draw points */
maxIterations = atoi( argv[1] );
#pragma omp parallel for shared(res,maxIterations) private(i,j,z,c,k,temp,lengthsq) schedule (dynamic,5)
for(i=0; i < Y_RESN; i++)
for(j=0; j < X_RESN; j++) {
z.real = z.imag = 0.0;
c.real = X_MIN + j * (X_MAX - X_MIN)/X_RESN;
c.imag = Y_MAX - i * (Y_MAX - Y_MIN)/Y_RESN;
k = 0;
do { /* iterate for pixel color */
temp = z.real*z.real - z.imag*z.imag + c.real;
z.imag = 2.0*z.real*z.imag + c.imag;
z.real = temp;
lengthsq = z.real*z.real+z.imag*z.imag;
k++;
} while (lengthsq < 4.0 && k < maxIterations);
if (k >= maxIterations) res[i][j] = 0;
else res[i][j] = 1;
}
printf("%d\n", res[0][0]);
/* Program Finished */
return 0;
}


