Effizienz
Effizienz
Die oft große Ökonomie in der Formulierung einer Lösung darf nicht darüber hinwegtäuschen, daß es erhebliche Kosten (Laufzeit, Speicherplatz) bei der Ausführung geben kann;
deshalb immer nötig:
- Anwendung allgemeiner Strategien (z.B. divide & conquer)
- Verständnis des Ausführungs- (Reduktions-) Prozesses
- Modellierung/Tests zur Lokalisierung von Problemen
die Funktion "`aslines"' in 3.6 wurde mit foldr definiert, kann aber in analoger Weise auch mit foldl abgestützt werden!
Unterschiede bei Definition:
Anhängen von rechts (ans Ende) des jeweils bereits gewonnen Teilergebnisses.
------------asLines: realisiert mit foldr und foldl
copy:: Int->a->[a] -Liste mit n-mal elem
copy (n+1) elem = elem : copy n elem
copy _ _ = []
break1:: Char->[[Char]]->[[Char]]
break1 c ls
|c == '\n' = [[]] ++ ls -new group
|otherwise = [[c]++(head ls)] ++ (tail ls) -add to group
asLines1:: [Char]->[[Char]]
asLines1 = foldr break1 [[]]
break2:: [[Char]]->Char->[[Char]]
break2 ls c
|c == '\n' = ls ++ [[]] -new group
|otherwise = (init ls) ++ [(last ls)++[c]] -add to group
asLines2:: [Char]->[[Char]]
asLines2 = foldl break2 [[]]
{---------------Beispielanwendungen asLines1/2:
Main> length (asLines1 (copy 1000 'a'))
1
(15023 reductions, 32026 cells)
Main> length (asLines2 (copy 1000 'a'))
1
(14023 reductions, 30026 cells, 1 garbage collection)
Main> length (asLines1 (copy 1000 '\n'))
1001
(19024 reductions, 32033 cells)
Main> length (asLines2 (copy 1000 '\n'))
1001
(518524 reductions, 1531533 cells, 17 garbage collections)
------------------------------}
| also: | im Falle von ' 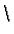 n' = Beginn neuer Zeile gewaltige Verschlechterung bei foldl-Version! n' = Beginn neuer Zeile gewaltige Verschlechterung bei foldl-Version! |
genauere Analyse sehr mühsam,
hier nur:
- Laufzeit (Reduktionen)
- einfacheres (aber ähnliches) Beispiel.
zur Erinnerung:
foldr 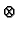 a [x1,...,xn]
a [x1,...,xn]
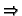 x1
x1 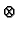 (foldr
(foldr 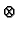 a [x2,...,xn]
a [x2,...,xn]
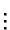
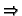 x1
x1 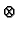 (x2
(x2 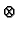 (...(xn
(...(xn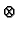 a)...))
a)...))
foldl 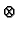 a [x1,...,xn]
a [x1,...,xn]
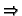 foldl
foldl  (a
(a  x1) [x2,...,xn]
x1) [x2,...,xn]
 (...((a
(...((a 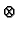 x1)
x1)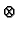 x2)
x2)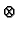 ...)...)
...)...)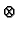 xn
xn
dann: wichtig, ob Operator  strikt ist oder nicht!
strikt ist oder nicht!
Beispiele:
| Addition (+) | = strikt |
| log. Und (&&) | = nicht strikt in 2.Argument, falls 1.Argument False: False && ? == False |
----------------------fold with strict op
Main> foldr (+) 0 [1..1000]
500500
(13020 reductions, 17032 cells)
Main> foldl (+) 0 [1..1000]
500500
(13020 reductions, 18032 cells)
--------------------fold with non-strict op
Main> foldr (&&) True [False,True,True,True,True,True,True,True,True,True]
False
(15 reductions, 31 cells)
Main> foldr (&&) True [True,True,True,True,True,False,True,True,True,True]
False
(25 reductions, 41 cells)
Main> foldr (&&) True [True,True,True,True,True,True,True,True,True,False]
False
(33 reductions, 49 cells)
Main> foldl (&&) True [False,True,True,True,True,True,True,True,True,True]
False
(34 reductions, 59 cells)
Main> foldl (&&) True [True,True,True,True,True,False,True,True,True,True]
False
(34 reductions, 59 cells)
Main> foldl (&&) True [True,True,True,True,True,True,True,True,True,False]
False
(34 reductions, 59 cells)
-------------------------------
Analyse:
Fall (+):  gleiche Effizienz!
gleiche Effizienz!
foldr (+) 0 [1,...,1000]
... 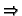 1+(2+ ...+(1000+0)...)
1+(2+ ...+(1000+0)...)
foldl (+) 0 [1,...,1000]
... 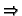 (...((0+1)+2)...)+1000
(...((0+1)+2)...)+1000
in beiden Fällen Aufbau des ganzen Ausdrucks, bevor erste Addition ...
(! lazy evaluation: Bei foldl werden die Teilsummen unausgewertet mitgeschleppt; es gibt eine Variante von foldl, die das nicht macht und in manchen Situationen besser ist)
Fall (&&): unterschiedliche Effizienz!
foldr (&&) True [True, ..., False, ..., True]
... 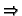 True && (...(False && (foldr (&&) True [True, ..., True])...)
True && (...(False && (foldr (&&) True [True, ..., True])...)
| aber: | False && "`irgendwas"' = False |
| d.h.: | fertig sobald False angetroffen |
foldl (&&) True [True, ..., False, ..., True]
... 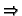 (...(...(True && True) && ...) && False) && ...)
(...(...(True && True) && ...) && False) && ...)
d.h.: erst ganzen Ausdruck aufbauen
------------------------Konkatenation
concTwo:: Int->Int
concTwo m = length ((copy m 'a') ++ "0123456789")
{------------------------Anwendungen:
Main> concTwo 1
11
(84 reductions, 121 cells)
Main> concTwo 10
20
(219 reductions, 346 cells)
Main> concTwo 100
110
(1569 reductions, 2597 cells)
Main> concTwo 1000
1010
(15069 reductions, 25098 cells, 1 garbage collection)
Main> concTwo 10000
10010
(150069 reductions, 250099 cells, 2 garbage collections)
------------------------------}
Zahlen lassen vermuten, daß Aufwand für (++) linear abhängt von Länge des linken Arguments;
in der Tat:
![$\left. \begin{array}{l} [] ++ ys = ys\ (x:xs)++ys = x:(xs++ys) \end{array} \right\} Def.\ (++)$](img34.gif)
d.h.
| (++) | braucht linkes (nicht rechtes) Argument und durchläuft dies elementweise, also Aufwand bestimmt durch Länge des linken Arguments! |
jetzt: fold zusammen mit (++):
--------------einfacheres foldr/foldl (++) Beispiel
right, left:: Int->Int
right m = length (foldr (++) [] (copy m "0123456789"))
left m = length (foldl (++) [] (copy m "0123456789"))
{-------------------Beispielanwendungen
Main> right 1
10
(90 reductions, 145 cells)
Main> right 10
100
(729 reductions, 1118 cells)
Main> right 100
1000
(7119 reductions, 10839 cells)
Main> right 1000
10000
(71019 reductions, 108040 cells, 2 garbage collections)
Main> left 1
10
(80 reductions, 116 cells)
Main> left 10
100
(1079 reductions, 2178 cells)
Main> left 100
1000
(55619 reductions, 156439 cells, 1 garbage collection)
Main> left 1000
10000
(5056019 reductions, 15064040 cells, 163 garbage collections)
-------------------------------}
| Vermutung: | right | linear |
| left | quadratisch |
Analyse:
(grob, unter Vernachlässigung von copy)
sei 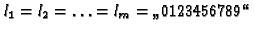
dann:
foldr (++) [] [l1, ..., lm]
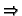 l1 ++ (foldr (++) [] [l2, ..., lm])
l1 ++ (foldr (++) [] [l2, ..., lm])
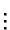
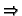 '0': ('1': ...('9': (foldr (++) [] [l2, ..., lm])...)
'0': ('1': ...('9': (foldr (++) [] [l2, ..., lm])...)
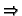 usw.
usw.
| also | (++) wird n-mal angewendet auf ein linkes Argument der Konstanten Länge 10, d.h. Schrittzahl 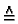 O(n) O(n) |
foldl (++) [] [l1, ..., lm]
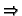 foldl (++) ([] ++ l1) [l2, ..., lm]
foldl (++) ([] ++ l1) [l2, ..., lm]
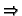 foldl (++) (([] ++ l1) ++ l2) [l3, ..., lm]
foldl (++) (([] ++ l1) ++ l2) [l3, ..., lm]
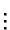
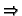 (...(([] ++ l1) ++ l2) ++ ...) ++ lm
(...(([] ++ l1) ++ l2) ++ ...) ++ lm
| also | (++) wird n-mal angewendet auf ein linkes Argument der wachsenden Länge 0, 10, 20, ..., (m-1)*10, d.h. Schrittzahl 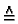 O(m2) O(m2) |






Next:Unendliche ListenUp:ListenPrevious:Beispiel: Text-Verarbeitung Ronald Blaschke
1998-04-19

