Beispiel: Newton-Approximation

Beispiel: Newton-Approximation

Das Verfahren zur Ermittlung einer Nullstelle einer Funktion f: R 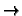R ist uns aus dem 1. Semester bekannt:

x₀ := geeigneter Startwert

x_i+1 := x_i - f(x_i)/f´(x_i)

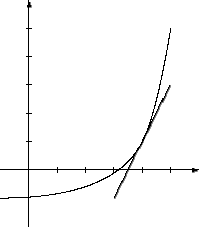
es gilt: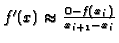

Das Verfahren ist wie geschaffen für imperative Programmierung:

• Iteration = Serie von Schritten, bis akzeptable Näherung gefunden
• Programmvariable = nehmen sich ändernde Werte von x auf

also interessant, ob man sowas -- und zwar gut! -- funktional erledigen kann!

Wir erinnern uns:

• Iteration läßt sich durch Rekursion ersetzen
• wobei Zwischenergebnisse als Resultate der Funktionsergebnisse "`unterwegs"' anfallen.

Daher die offensichtliche Lösung:

 newton :: (Float->Float)->Float->Float

newton f x

   |abs(f x) < 0.001 = x  - Feierabend wenn gut genug

   |otherwise        = newton f (x - f x / diff f x) - weiter

Anwendung z.B. so:

 Main> newton (\x->x^2-2) 10  -loest x^2-2 = 0, d.h. Wurzel 2, Start bei 10

1.41454

Hat man erst eine Programmieraufgabe gelöst, so sollte man gleich fragen, ob sich die Lösung verallgemeinern läßt, d.h. gibt es hier eine Struktur, ein Muster, das mehrfach angewendet werden kann?

Bestandteile der Lösung sind:

• ein Ausgangswert: x
• eine den aktuellen Wert verbessernde Berechnung: (x - f x / diff f x)
• ein Wiederholungsmechanismus: rekursiver Aufruf
• ein Abbruchkriterium

Idee:

Mache aus dem Wiederholungsmechanismus eine Funktion, die die drei anderen Bestandteile als Parameter hat!

Daher definiere:

 until :: (a->Bool)->(a->a)->a->a

           |          |     |  |-- Ergebnis

           |          |     |-- Startwert

           |          |-- Verbesserung

           |-- Abbruchkriterium

Und natürlich a = Typvariable, d.h. egal, in welchem Wertebereich wir arbeiten, also polymorphe Funktion.

 repeat_until::(a->Bool)->(a->a)->a->a

repeat_until crit change x

   |crit x    = x                                   -zufrieden

   |otherwise = repeat_until crit change (change x) -weiter

Einfaches Anwendungsbeispiel:

 Main> repeat_until even pred 10

10

Main> repeat_until even pred 11

10

Wobei die Standardfunktionen

 even :: Int -> Bool     - "ist gerade"

pred :: Int -> Int      - "Vorgänger"

vorhanden sind.

Jetzt damit zurück zu Newton:

 newton :: (Float->Float)->Float->Float

newton f x = repeat_until n_crit n_change x

where n_crit x = abs(f x) < 0.001

n_change x = x - f x / diff f x

Anwendung für Quadratwurzelberechnung:

 Main> newton (\x->x^2-2) 10

1.41454

Main> newton (\x->x^2-25) 10

5.0

Main> newton (\x->x^2-80) 10

8.94427

usw.

• Man kann die Suche noch flexibler machen, insbesondere bessere Abbruchkriterien einführen, die auf Vergleich von 2 (oder mehr) der aufeinanderfolgenden Näherungswerte beruhen;

  Kapitel 3: Listen

• Man kann Nullstellenberechnung auch benutzen, um die inverse Funktion zu einer Funktion f numerisch zu ermitteln:

  
  

  
  
  

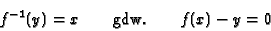
  Das leistet die folgende Definition:

   inverse:: (Float->Float)->Float->Float->Float
  
  inverse f y x = newton g x
  
  where g x = f x - y   
  
  

  Einfache Anwendungen sind wieder Wurzelprobleme:

   Main> inverse (\x->x) 2 10
  
  2.0
  
  Main> inverse (\x->x^2) 2 10
  
  1.41454
  
  Main> inverse (\x->x^3) 2 10
  
  1.25993
  
  Main> inverse (\x->x^4) 2 10
  
  1.18925
  
  Main> inverse (\x->x^10) 2 10
  
  1.07179
  
  
  

  usw.

Beachte:

Anwendung der Newton-Iteration hat ihre mathematischen Grenzen, und man muß sich für wirklich gute Ergebnisse auch noch in der numerischen Mathematik auskennen und Sorgfalt hinsichtlich Startwerten, Abbruchkriterien, genaue Formulierungen des Iterationsschritts ... walten lassen!